BaekJoon 백준 2167 2차원 배열의 합 문제는 2차원 배열이 주어졌을 때 (i, j) 위치부터 (x, y) 위치까지에 저장되어 있는 수들의 합을 구하는 문제이다. 반복적 구조로 푸는 방법과 DP, 메모이제이션 기법을 사용한 2가지 방식이 있다. 난이도는 Bronze 1이다.
BaekJoon 2167 2차원 배열의 합 문제 정보
출처
- https://www.acmicpc.net/problem/2167
알고리즘 분류
- 동적 계획법 DP; Dynamic Programming, 메모이제이션 memoization
난이도
- 브론즈 1 / Bronze 1
2차원 배열의 합 문제 요약
- 배열의 크기 N, M (1 ≤ N, M ≤ 300)인 2차원 배열이 주어진다.
- 배열에 포함되어 있는 수는 절댓값이 10,000보다 작거나 같은 정수이다.
- (i, j) 위치부터 (x, y) 위치까지에 저장되어 있는 수들의 합을 구하여 출력한다.
- 배열의 (i, j) 위치는 i행 j열을 나타낸다.
문제 풀이 과정
- 이차원 리스트에 입력받은 정수를 저장한다.
- 동적 계획법의 메모이제이션 방법을 사용하기 위해 memo 2차원 리스트를 선언합니다.
- memo에 arr의 (0, 0)부터 (a, b)까지의 합을 저장합니다.
- memo의 값을 이용하여 (i, j)부터 (x, y)까지의 합을 구하여 출력합니다.
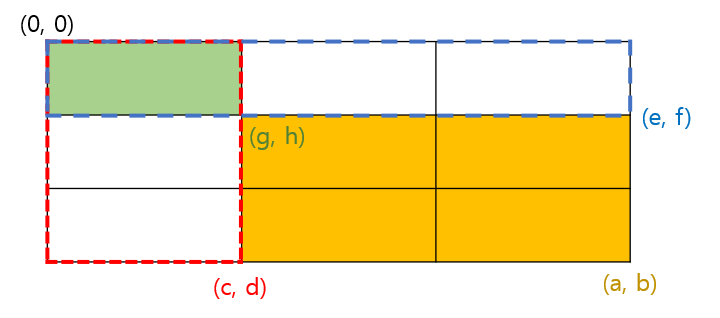
(g, h)에서 (a, b)까지의 합을 구하는 공식 >
(0, 0)~(a, b)까지의 합 - (0, 0)~(c, d)까지의 합 - (0, 0)~(e, f)까지의 합 + (0, 0)~(g, h)까지의 합
코드 및 설명
- arr [][] - 정수가 저장되어 있는 2차원 리스트
- memo [][] - arr의 (0, 0)부터 (a, b)까지의 합을 저장해 놓은 2차원 리스트
N, M = map(int, input().split())
arr = []
for _ in range(N):
arr.append(list(map(int, input().split())))
memo = [[0] * (M + 1) for _ in range(N + 1)]
for m in range(1, N + 1):
for n in range(1, M + 1):
memo[m][n] = memo[m][n - 1] + memo[m - 1][n] - memo[m - 1][n - 1] + arr[m - 1][n - 1]
K = int(input())
for _ in range(K):
i, j, x, y = map(int, input().split())
print(memo[x][y] - memo[i - 1][y] - memo[x][j - 1] + memo[i - 1][j - 1])
처음에는 반복문을 이용한 반복 구조로 구현했는데, 답은 나오지만 시간 초과가 발생했습니다.
이러한 반복적 구조의 시간문제를 보완한 프로그래밍 기법이 바로 메모이제이션 기법인데요, 성능, 실행 속도 향상을 위해 중요한 기술이고, 동적 계획법은 메모이제이션을 사용하여 구현한 알고리즘입니다. 한 번 읽어보시면 큰 도움이 될 것입니다.
DP Dynamic Programming 동적 계획법 알고리즘과 예제
DP Dynamic Programming 동적 계획법 알고리즘과 예제
포스팅에서 다룰 DP; Dynamic Programming 동적 계획법 알고리즘은 큰 문제를 여러 개의 작은 문제들로 나누어 푸는 방법으로 최적화 문제를 해결하고 프로그램의 전체적인 실행 속도와 성능을 향상할
wondytyahng.tistory.com
메모이제이션(Memoization) 개념 및 예시, 재귀(recursion)
메모이제이션(Memoization) 개념 및 예시, 재귀(recursion)
이번 포스팅에서 다루는 memoization 메모이제이션은 DP 동적 계획법 알고리즘에서 핵심이 되는 기술로 중복 계산을 제거함으로써 프로그램의 전체적인 실행 속도를 빠르게, 성능을 향상할 수 있
wondytyahng.tistory.com
BaekJoon 백준 2167 2차원 배열의 합 문제를 파이썬 python으로 동적 계획법 dp 알고리즘의 memoization 메모이제이션 기법을 사용하여 풀어보았다. 난이도는 Bronze 브론즈 1이다.
'Algorithm Problem Solving > BaekJoon' 카테고리의 다른 글
| [BaekJoon] 백준 1259 팰린드롬 수 (Python / 파이썬) (0) | 2021.08.17 |
|---|---|
| [BaekJoon] 백준 1032 명령 프롬프트 (Python / 파이썬) (0) | 2021.08.16 |
| [BaekJoon] 백준 2748 피보나치 수 2 (Python / 파이썬) (0) | 2021.08.16 |
| [BaekJoon] 백준 2869 달팽이는 올라가고 싶다 (Python / 파이썬) (0) | 2021.08.15 |
| [BaekJoon] 백준 1924 2007년 (Python / 파이썬) (0) | 2021.08.15 |
댓글